Geometry: Area and Perimeter
1.Triangle :
Answer:(1) comparing area of any figure with the help of different objects like palm, leaf, pencil, notebook, etc.
Q4 .The concept of areas of plane figures can be introduced to the students of Class V by
1.Triangle :
Area of triangle = (1/2) x b x p
Where,
b = the length of the side where perpendicular is drawn from opposite
point
p = the length of the perpendicular
Perimeter of triangle :
Perimeter of a triangle = (a + b + c),
where,
a, b, c are the length of the sides AB, BC and AC.
2. Rectangle : A rectangle is a parallelogram, whose opposite sides are equal and the angle at which the lines intersect is 90. The diagonals of the rectangle are equal in length.
Area of rectangle = l x b
where,
l = length of rectangle
b = breadth of rectangle
Perimeter of rectangle = 2 ( l + b )
where,
l = length of rectangle
b = breadth of rectangle
Diagonal of a rectangle is a line segment joining two opposites vertices of the rectangle.
Relationship of the diagonal to the sides of rectangle:
______
diagonal =√l² + b²
3. Square : A square is a rectangle, whose all sides are equal. Diagonal of a square are perpendicular bisector of each other.
Area of square = l x l
where l = length of one side
Perimeter of square = 2 ( l + l ) = 4 l
Diagonal of a square is a line segment joining two opposites vertices of the square.
______ __
diagonal =√l² + l² = l√2
4. Rhombus: A rhombus is a parallelogram, whose all sides are equal.
 |
| Rhombus with side "a" and diagonals d1 and d3 |
Area of rhombus = (1/2) x d1 x d2
where d1 = length of shorter diagonal
d2 = length of larger diagonal
Perimeter of rhombus = 2 ( a + a ) = 4 a
Solved Problems
Q1. The length of a rectangle is ‘l’ and its width is half of its length. What will be the perimeter of the rectangle if the length is doubled keeping the width same ?
(1) 4l
(2) 5l
(3) 6l
(4) 3l
(2) 5l
(3) 6l
(4) 3l
Answer: (2) 5l
Solution: Here,for first rectangle length = l and the width = (l/2). A
new rectangle is formed by keeping the width same i.e (l/2) and doubling the length i.e. 2l .
therefore, perimeter becomes = 2( 2l + l/2)
= 2(5l/2)
= 5l
Q2 To introduce the concept of area, a teacher can start with
(1) comparing area of any figure with the help of different objects like palm, leaf, pencil, notebook, etc.
(2) calculating area of a rectangle by finding length and breadth of a
rectangle and using the formula for area of a rectangle (i.e. length x breadth)
(3) calculating area of figures with the help of counting unit square
(4) explaining of formulae for finding area of figures of different shapes
Answer:(1) comparing area of any figure with the help of different objects like palm, leaf, pencil, notebook, etc.
Q3. A rhombus has diagonals of length 8 cm and 6 cm. Find its perimeter.
(1) 18 cm
(2) 20 cm
(3) 24 cm
(4) 28 cm
Answer:(3) 24 cm
Explanation: Area of rhombus = (1/2 )x d1 x d2 ,
where d1 and d2 are the two the diagonal of a rhombus.
here, d1 = 8, d2=6, Therefor, area = (1/2) X 8 X 6 =48/2 = 24
Q4 .The concept of areas of plane figures can be introduced to the students of Class V by
(1). calculating the area of a rectangle by finding length and breadth of a rectangle and using the formula for area of a rectangle
(2) stating the formula for area of rectangle of rectangle and square
(3). calculating the area of figures with the help of counting unit squares.
(4). measuring the area of any figure with the help of different objects like palm, leaf, pencil etc.
Answer: (1) Δ PQR ≡ TRQ
Solution: In each option, compare the triangles on the left and the right of the similarity symbol, for similar angles and sides. For example taking option (1), the angle QRP and similarly taking angle from the other triangle it will be angle RQT and they are equal. Similarly comparing each sides and angles, we will confirm that option (1) is correct.
Answer:(3). calculating the area of figures with the help of counting unit squares.
Q5: The figure consists of five squares of the same size. The area of the figure is 180 square centimeters. The perimeter (in cm) of the figure will be
(1) 48
(2) 72
(3) 36
(4) 45
(1) 48
(2) 72
(3) 36
(4) 45
Answer: (2) 72
Explanation: The area of the total figure = 180 sq. cm. Since it is made up of 5 identical square, the area of one square will come out be = 180/5 = 36 sq.cm. And the length of the square will work out to be = √36 = 6 cm.
Now, going around the figure we will see, that there are 12 sides in total of al the square that makes the perimeter of this figure.Hence, the perimeter would come out to be 12 x 6 = 72
Q6
Explanation: The area of the total figure = 180 sq. cm. Since it is made up of 5 identical square, the area of one square will come out be = 180/5 = 36 sq.cm. And the length of the square will work out to be = √36 = 6 cm.
Now, going around the figure we will see, that there are 12 sides in total of al the square that makes the perimeter of this figure.Hence, the perimeter would come out to be 12 x 6 = 72
Q6
Answer: (4) 4
Q7:
Answer: (2) 120
Solution: Since it is given that <d = (1/2) <E. And both angle D and angle E are two angle of right angled triangle CED. We have,
∠D + ∠E + 90° = 180°
=> ∠D + 2∠D = 180° -90°
=> 3∠D = 90°
=> ∠D = 90° x (3)
=> ∠D = 30°
Also, it is given that (1/2)∠A = ∠D
=> ∠A = 60° = ∠B ( since CA and CB are equal and so
are angle)
And therefore, ∠ BCA = 60°
But ∠ BCA + ∠ACD = 180° => ∠ACD = 180° - 60° = 120°
Q8.
Solution: In each option, compare the triangles on the left and the right of the similarity symbol, for similar angles and sides. For example taking option (1), the angle QRP and similarly taking angle from the other triangle it will be angle RQT and they are equal. Similarly comparing each sides and angles, we will confirm that option (1) is correct.
Q9. Perimeter of a square is 24 cm and the length of the rectangle is 8 cm.If the perimeters of the square and the rectangle are equal , then the area of the rectangle is
(1) 16
(2) 24
(3) 32
(4) 64
Answer: (3) 32
Solution:
Since perimeter of the square and rectangle are equal, then
4S = 2( L + B)
where, 4S = 24, L = 8cm.
Put the values to get
24 = 2(8 + B)
=>12 = 8 + B
=>4 = B
Therefore area of the square is = 4 x 8 = 32 square cm
Q10 : The perimeter of the square is 20 cm. A rectangle has the same width as the square. The length of the rectangle is twice the width. The area in ,square cm, of the rectangle is :
(1) 30
(2) 50
(3) 100
(3) 100
(4) 25
Answer: (2) 50
Solution:
Perimeter of the square = 20 cm
Therefore length of the side of the square = 20/4 = 5cm
A rectangle has the same width as the side of the square. So, width of the rectangle is 5 cm and since it length is double the width, the length comes out to be 10 cm.
Therefore area of rectangle = l x b = 5 x 10 =50 square cm






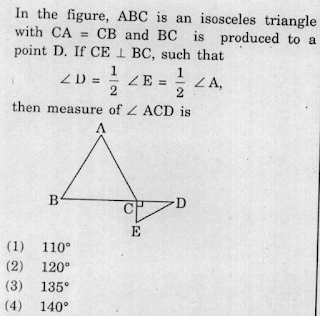

No comments:
Post a Comment